Shortest Distance Calculation No Sweat for this Road ‘Oracle’

(Hyperific/Shutterstock)
As big data analytics takes to the roads, the need for accurate distance calculations has blossomed too. However, traditional approaches to this problem face considerable challenges with accuracy and scalability. Now a group of researchers out of the University of Maryland at College Park think they found have an accurate and scalable solution with their Distance Oracle.
Roads may seem like a pedestrian topic for big data analytics. After all, roads are just strips of concrete or asphalt that we use to drive from one place to another. What’s so complicated about that?
But roads are surprisingly complex when considered in aggregate. When you consider that this country has more than one million named roads, constituting more than 4 million miles of paved byways, you begin to understand the massive scale and complexity of our road network.
Anybody who traverses the roads for business or pleasure has a need to calculate the distances they’ll travel. Whether it’s a Blue Apron driver delivering a meal in a big city or a family headed to the beach for Memorial Day, the number of miles on the route between points A and B is a fundamental number that will impact many aspects of the journey.
The simplest way to calculate distance is to put a ruler down against a paper map. This Euclidian distance will be useful when we all have self-flying cars, but until then its usefulness will be limited mainly to crows. It may surprise you, however, to know that many online services, including Google Maps, often utilize the Euclidian distance when a user submits a common query like “Where are the 10 closest Chinese restaurants?”
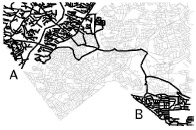
An example of path coherence of a road networking in Silver Spring, Maryland, as originally published in “Roads Belong in Databases” from the Bulletin of the IEEE Computer Society Technical Committee on Data Engineering.
The more useful number is the distance we’ll travel across the existing roads. A graph database can be a useful tool for calculating this distance. If you transposed the roads into a graph database, and considered every intersection of two roads (sometimes three) to be a vertex (or node), one could then use a shortest distance algorithm, such as Dijkstra’s algorithm, to find the shortest distance between two vertices.
While this approach works and is accurate, it’s computationally expensive and therefore not scalable. If you wanted to calculate the distances between 1,000 different places (or vertices in graph speak), then you’d have 1,000 times 1,000, or potentially up to 1 million, paths to check. And the amount of space you’d need to compute that would be N cubed, or a billion.
“This is for a small problem,” says University of Maryland Computer Science Professor Hanan Samet. “If you look at a road network of the United States, it has about 24 million vertices. These numbers get way beyond anything you can conceive of.”
Professor Samet and two of his students at the University of Maryland’s Institute for Advanced Computer Studies, Jagan Sankaranarayanan and Shangfu Peng, worked on this problem and came up with what they believe is a groundbreaking solution that could find application in any number of real-world big data analytic problems companies are facing today.
The solution boils down to precomputing distances between two points in an intelligent manner, storing the results in an SQL table, and then figuring out how to serve the distance values very quickly.
A straightforward attempt to calculate the distance between every two points on this continent is a fool’s errand. This brute force approach would be too costly and slow to have much use at all. The College Park researchers got around this problem in a clever way: grouping nearby vertices with similar distances from another group of nearby vertices dramatically reduces compute and storage requirements.
“We take advantage of what we call space coherence to dramatically reduce the number of pairs of vertices , or vertex groups, the distance between which is needed to answer a query,” Professor Samet tells Datanami. “
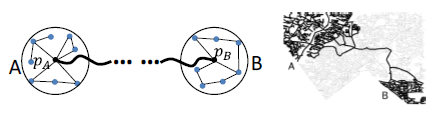
Example of a well-separated pair of locations in Silver Spring, from CDO: Extremely High-Throughput Road Distance Computations on City Road Networks, published in Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems
“Here’s an example,” he continues. “Suppose I’m in New York and I’m going to California. If you look at it, for every point in New York and every point in California, the shortest path between them usually goes through a common point. Think about a dumbbell. You can view California as one disk [of the dumbbell] and New York as another disk. So you see, the distances between the points on the two disks are not going to be different by a lot, and the shortest path between them will go through a common point.”
Depending on the extent of the user’s error tolerance, the number of pairs needed can be raised up or down. Most of the early tests show that the researchers can get an error rate of 1% to 2% with a reasonably sized data set. For example, the relational database table that represents the entire United States road network was 500 GB. That table took 50 servers on AWS about eight hours to compute. Once it’s been computed, it’s simply a matter of querying the table through SQL to get the answer.
Sankaranarayanan, who is no longer at University of Maryland, says this piece of technology, which he calls Distance Oracle, essentially transforms distance computation from a search problem into a retrieval problem
“We had this idea to take the whole United States road network and just precompute the hell out of it,” he tells Datanami. “Just precompute the shortest path and distance between every location in the United States to every other location in the United States. I can precompute it, and can store it in a very compact representation, so that when you give me a query, I don’t have to do a graph traversal. I have the answer ready right in front of me. I just have to retrieve the answer and give it to you.”
Equipped with the Distance Oracle, a single commodity machine can respond to 10 million queries per second, according to a best demo paper award winning article co-written by Peng and Samet, titled “CDO: Extremely High-Throughput Road Distance Computations on City Road Networks,” published November 2016 in the Proceedings of the SIGSPATIAL Conference, a publication of the ACM Special Interest Group on Spatial Information.
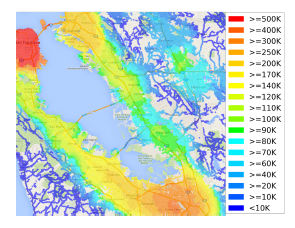
A graph showing nearby job opportunities within 10 kilometers, calcluated for each census block in the San Francisco Bay Area. It required 120 million distance, which the Road Oracle completed in 18 seconds (from the paper “CDO: Extremely High-Throughput Road Distance Computations on City Road Networks” published in Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems).
By comparison, the graph traversal approach tops out at around 5,000 requests per second. “That’s a dramatic difference,” Sankaranarayanan says. “You’re going from 5,000 to 10 million. That’s on a single machine. The reason is that you’re not doing any search. You’ve precomputed every answer beforehand. All I’m doing is retrieving r it and giving it to you.”
The Distance Oracle could potentially be used anytime a distance calculation is needed. National parcel delivery companies could be potential users, as could local food delivery companies or even ride-sharing outfits.
The technology could also be used with location-based advertising that’s targeted and done in real time. Imagine that, as you’re driving to work, you receive a coupon for a dollar off a coffee at a restaurant that’s relatively close to your normal route. A Euclidian distance-based approach could be far off the mark, whereas the Distance Oracle could give a much more accurate estimate of the distance between you and the restaurant.
Real estate is another potential use case. A house-hunter may be interested in miniimizing the sum of the distances between their office and their child’s school. “Distance turns out to be a very important decision factor influencing many things we do,” Professor Samet says.
Professor Samet and Pengare in the process of developing a business plan around the Distance Oracle. The technology is done, and it’s been patented, but displacing existing distance-calculation methods may take some time.